Lavoro ed energia
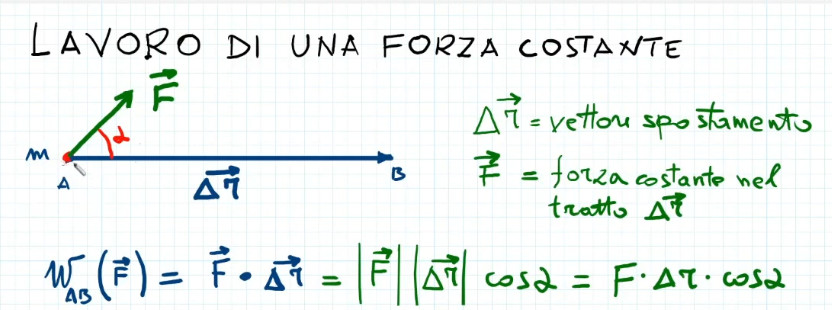
Nel video seguente definiremo la grandezza fisica lavoro (work in inglese). Si inizia con il semplice caso di forza costante lungo un tratto rettilineo:
$$ W_{AB}(\vec F) = \vec F \cdot \Delta \vec r $$
per passare al caso generale di forza arbitraria e percorso curvilineo $\gamma$ anch’esso arbitrario:
$$ W_{AB}(\vec F) = \int_\gamma \vec F \cdot d \vec r $$
e arrivare, infine, alla circuitazione, cioè al caso in cui il percorso sia chiuso
$$ W_{AB}(\vec F) = \oint_\gamma \vec F \cdot d \vec r $$
Il video successivo introduce il teorema dell’energia cinetica. Esso dichiara la validità della seguente relazione per qualsiasi tipo di forze
$$ W_{AB}(\vec F) = \frac{1}{2} m v_B^2 - \frac{1}{2} m v_A^2 $$
in cui la quantità $ E_k = m v^2 / 2 $ è nota come energia cinetica.
Se le forze agenti sul punto materiale dipendono dalla posizione e verificano la seguente relazione per qualsiasi curva $\gamma$
$$ W_{AB}(\vec F) = \oint_\gamma \vec F \cdot d \vec r = 0$$
allora si può scrivere anche la seguente relazione
$$ W_{AB}(\vec F) = E_{pA} - E_{pB} $$
in cui la quantità $ E_p $ è nota come energia potenziale e la sua espressione dipende dal tipo di forza considerata. Ecco un piccolo promemoria ($\vec K=(K_x,K_y,K_z)$ è un vettore costante, e $k$ è una costante numerica):
| Forza | Energia potenziale |
|---|---|
| $\vec K$ | $-\vec K \cdot \vec r $ |
| $ K_x \vec i$ | -$ K_x x $ |
| $ K_y \vec j$ | -$ K_y y $ |
| se $ K_y = -mg$, allora $ -mg \vec j$ | $ mg y $ |
| $ -k x \vec i$ | $ k x^2/2 $ |
| $k/ x^2 \vec i$ | $ -k/x $ |
Per le forze conservative i precedenti risultati possono essere combinati per ottenere il teorema di conservazione dell’energia meccanica totale. Si può scriverlo in diverse forme equivalenti:
$$ E_{kB} - E_{kA} = E_{pA} - E_{pB} $$
$$ E_{kB} + E_{pB} = E_{kA} + E_{pA} $$
$$ E_k + E_p = costante $$
Il risultato precedente, $ W_{AB}(\vec F) = E_{pA} - E_{pB} $, sottende una precisa relazione tra la forza e la sua energia potenziale. In particolare abbiamo la seguente relazione fondamentale
$$ \vec F_{media} = - \frac{\Delta E_p}{\Delta r_{AB}} $$
ovvero
$$ \vec F = - \frac{d E_p}{d r} $$

