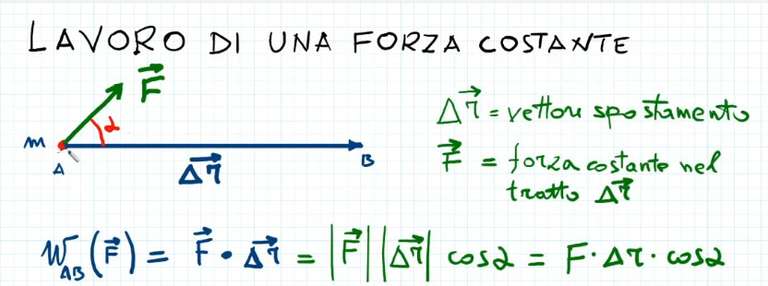
Lavoro termodinamico

Col termine lavoro termodinamico o semplicemente lavoro, intendiamo quella quantità di energia scambiata dal sistema (acquistata o ceduta) che possiamo calcolare come abbiamo imparato in meccanica, cioè attraverso il prodotto forza per distanza. Il lavoro sarà positivo quando produrrà un aumento di energia interna, e negativo se produrrà una diminuzione di energia interna (questa naturale convenzione è opposta a quella tradizionale basata su applicazioni ingegneristiche). Nel primo è l’ambiente esterno a compiere lavoro sul sistema, mentre nel secondo caso avviene il contrario.

Alcuni tipi di forze producono variazioni di volume del sistema. In questo caso parleremo di lavoro meccanico. Altre forze non producono variazioni di volume ma potrebbero cambiare le proprietà elettriche o magnetiche del sistema. Parleremo in quest’ultimo caso di lavoro elettromagnetico. In generale l’espressione del lavoro termodinamico tiene conto di tutti i possibili contributi.

Qualora il sistema sia un gas contenuto in un cilindro con un pistone mobile di superficie $S$ e soggetto ad una pressione $p$ esterna, in corrispondenza di una piccolo spostamento $dx$ del pistone, il lavoro meccanico elementare è dato da

$$\delta W = F dx = p S dx = p dV$$

dove $dV$ è la variazione di volume subita dal cilindro. Nota che si è usato il simbolo $\delta W$ il cui equivalente macroscopico non è $\Delta W$. Infatti non avrebbe senso scrivere $\Delta W= W_{finale}-W_{iniziale}$ non esistendo una funzione lavoro. Quindi il lavoro totale tra due stati termodinamici $A$ e $B$ lo indicheremo, come al solito, con

$$W_{AB} = \int_A^B p dV$$

Nel precedente integrale si noti che il risultato dipende dalla trasformazione seguita per andare dallo stato $A$ allo stato $B$. In altri termini, $p$ in generale non è una costante ma potrebbe variare lungo la trasformazione. Esempi di calcolo del lavoro verranno mostrati più avanti a proposito del gas perfetto.

Un altro modo di eseguire lavoro è inserire nel sistema gassoso o liquido delle ventole/pale messe in rotazione dall’esterno (proprio come nei frullatori) alimentate in vario modo, per esempio facendo cadere dei pesi, oppure in modo elettrico. Il lavoro durante la caduta dei pesi è calcolabile tramite il prodotto forza peso per distanza e lo ritroviamo come aumento di energia interna. Il lavoro prodotto dalle pale se alimentato elettricamente può essere dedotto leggendo dal contatore l’energia impiegata e che poi pagheremo in bolletta.

Un altro modo di produrre lavoro è attraverso una resistenza elettrica alimentata dall’esterno con una batteria. In questo caso entrano in gioco forze elettromagnetiche e tale lavoro si sa misurare ($W=\Delta V I \Delta t$).

Pareti e trasformazioni adiabatiche

Se un sistema è delimitato da pareti adiabatiche allora intendiamo dire che non esiste trasferimento termico. In questo caso, durante la trasformazione termodinamica, ora detta adiabatica, il termine $Q$ varrà sempre zero.

Le pareti perfettamente adiabatiche nella realtà non esistono. Infatti è impossibile garantire $Q=0$ quando l’ambiente esterno si trova ad una temperatura diversa da quella del sistema. I comuni thermos casalinghi rappresentano il tentativo di riprodurre un contenitore adiabatico. Sappiamo bene che la loro capacità di mantenere i corpi alla stessa temperatura diminuisce al passare del tempo. In genere, una buona approssimazione ad una trasformazione adiabatica, è quella che avviene in un tempo molto breve. Infatti, durante questo piccolo intervallo di tempo, i meccanismi microscopici che sottostanno al termine $Q$ producono effetti trascurabili.

I fondamentali esperimenti di James Joule con le trasformazioni adiabatiche dimostrarono che le medesime quantità di lavoro $W$, ma prodotte con modalità diverse (meccaniche, elettriche,…) producono un aumento di temperatura $\Delta T$ in acqua che verifica la seguente relazione

$$W = J m \Delta T$$

in cui $m$ è la massa dell’acqua in kg, e $J =4186$ Joule/(kg °C). In altri termini, Joule dimostrò che occorrono 4,186 joule di energia per far aumentare di 1 grado centigrado la temperatura di una massa d’acqua di 1 grammo. Usando sostanze diverse al posto dell’acqua si ottiene una relazione simile ma con altre costanti.

Il video seguente mostra una macchina simile a quella usata da Joule per i suoi esperimenti ma non porta a termine i calcoli

Su alcuni libri si usa il termine energia termica senza una sua chiara definizione suggerendo erroneamente l’introduzione di una nuova energia e creando confusione. Uno dei pochi libri in cui essa è chiaramente definita è quello di Chabay e Sherwood. Gli autori associano tale termine a quella parte dell’energia interna del sistema che il sistema acquista o cede in corrispondenza di una variazione di temperatura $\Delta T$ del sistema. Tuttavia noi non useremo affatto tale termine per non suggerire involontariamente l’introduzione di una nuova forma di energia.

Bibliografia

Matter & Interactions, Ruth W. Chabay, Bruce A. Sherwood, John Wiley & Sons Inc; 4° edizione (2014)