Trasferimento termico

L’aumento di temperatura di un sistema può avvenire anche nei casi in cui $W=0$. In questo caso il processo responsabile è quello che abbiamo denotato come trasferimento termico o lavoro microscopico e indicato con $Q$. Per metterlo in atto il sistema deve comunicare con l’ambiente esterno, o con un altro sistema, attraverso una parete diatermica, cioè una parete che non consente il passaggio di materia ma solo di energia quando ai suoi lati esiste una differenza di temperatura. Quindi, nel caso $W=0$, il I principio permette di scrivere

$$\Delta U = Q$$

Come applicazione di ciò si considerino due sistemi isolati aventi rispettivamente temperature $T_1$ e $T_2$ con $T_1<T_2$. Per ognuno di essi $W=Q=0$ e quindi $\Delta U_1=\Delta U_2=0$. Ora si immagini di metterli in contatto termico attraverso una parete fissa diatermica.

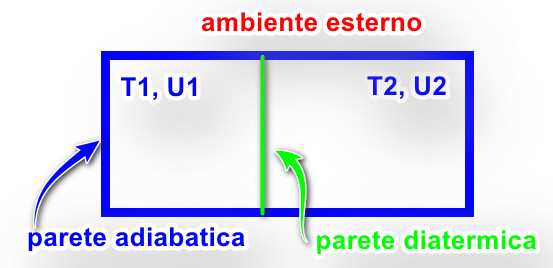
In questo caso il nuovo sistema risultante continua ad essere isolato dall’ambiente esterno per cui avremo $U_1+U_2=costante$. Tuttavia sarà permesso il trasferimento termico dal sistema a temperatura maggiore a quello a temperatura minore. Poiché le variazioni di volume dei due sistemi saranno nulle, allora il termine $W$ vale 0 per ciascun sistema, mentre varieranno le energie interne dei due sistemi. A seguito di ciò anche le temperature dei due sistemi varieranno e si raggiungerà l’equilibrio termico alla temperatura $T_e$. Quindi avremo

$$\Delta U_1 + \Delta U_2=0 $$

da cui

$$Q_1 + Q_2 =0$$

Per la quantificazione del termine $Q$, cioè per la sua misura, si può ricorrere a quanto imparato nel paragrafo precedente a proposito degli esperimenti di Joule. Il corpo di massa $m$ che ha acquistato l’energia $Q$ si può mettere a contatto con una quantità di acqua di massa nota $m_a$ e all’equilibrio termico si registra la variazione di temperatura $\Delta T_a$ dell’acqua e $\Delta T_c$ del corpo. Quindi con l’apparato di Joule si esegue lavoro per determinare quale quantità di lavoro sarà capace di produrre la stessa variazione di temperatura $\Delta T_a$ sulla medesima massa di acqua, ottenendo la $W=Q$.

Gli esperimenti mostrano la validità della seguente relazione

$$Q = c m \Delta T_c \tag{1}$$

in cui $c$ è una grandezza che dipende dalla sostanza usata e prende il nome di capacità termica specifica della data sostanza. Invece la quantità $C=cm$ prende il nome di capacità termica del corpo. Se si riscrive la precedente relazione come

$$c = \frac{Q}{ m \Delta T} \tag{2}$$

si vede che la capacità termica specifica è l’energia che un corpo di massa unitaria deve acquistare per trasferimento termico per aumentare la propria temperatura di 1 °C.

Riprendendo il problema iniziale, per i due corpi in equilibrio termico, potremo scrivere

$$c_1 m_1 (T_e-T_1)+c_2 m_2 (T_e-T_2)=0$$

da cui si può ricavare la temperatura di equilibrio note tutte le altre grandezze. La precedente relazione viene usata negli strumenti chiamati calorimetri proprio al fine di determinare le capacità termiche specifiche di sostanze sconosciute e verranno studiati nel seguito. Il precedente risultato si può generalizzare ad un numero arbitrario di sistemi con gli stessi vincoli.

Caso generale

Nel caso generale il sistema può subire/svolgere sia lavoro che essere soggetto a trasferimento termico (acquista o cede energia a causa di una differenza di temperatura con l’ambiente esterno). In tal caso occorre usare l’espressione completa del I principio

$$\Delta U = W + Q$$

Le quantità $W$ e $Q$ dipendono dal tipo di trasformazione tra due stati termodinamici sebbene non lo sia la funzione $U$. Vedremo più avanti che esistono dei sistemi costruiti per funzionare ciclicamente e che prelevano energia per trasferimento termico e la trasformano in lavoro meccanico. Si tratta ovviamente di macchine che hanno una importanza tecnologica fondamentale per lo sviluppo industriale. L’interesse per la termodinamica ebbe come impulso proprio la comprensione del funzionamento di queste macchine e dei limiti teorici per ottenerne la massima efficienza.

Capacità termiche specifiche particolari

La quantità $Q$ di trasferimento termico subito da un sistema dipende dal tipo di trasformazione eseguita. In ogni caso vale la relazione $\Delta U = Q + W$ per cui la relazione (2) si può scrivere come

$$c = \frac{Q}{ m \Delta T} = \frac{ \Delta U - W}{ m \Delta T} = \frac{ \Delta U - p \Delta V}{ m \Delta T} \tag{3} $$

Nella quale per il lavoro ci siamo limitati a quello meccanico di espansione. Fra le varie possibili trasformazioni ve ne sono due di particolare interesse: a volume costante e a pressione costante.

Nel caso di una trasformazione a volume costante allora $W=0$ e avremo la capacità termica specifica a volume costante

$$c_V = \frac{Q}{ m \Delta T} = \frac{ \Delta U}{ m \Delta T} \tag{4}$$

Nel caso della trasformazione a pressione costante allora avremo la capacità termica specifica a pressione costante

$$c_P = \frac{Q}{ m \Delta T} = \frac{ \Delta U - p \Delta V}{ m \Delta T} \tag{5} $$

Si noti che $c_P > c_V$ in quanto, a pressione costante, il sistema si espande e compiendo lavoro tende a raffreddarsi, cioè, per produrre nel sistema un aumento di temperatura di 1 °C, occorre un trasferimento termico maggiore che a volume costante.

Bibliografia

Fisica. Meccanica, termodinamica, Paolo Mazzoldi , Massimo Nigro, Cesare Voci, Edises, seconda edizione, 1998

Matter & Interactions, Ruth W. Chabay, Bruce A. Sherwood, John Wiley & Sons Inc; 4° edizione (2014)