Retta di regressione

Il video seguente introduce il problema e fornisce delle formule risolutive quando si vuole cercare una ‘’relazione lineare’’ tra due grandezze fisiche. Il grafico della relazione lineare è una retta detta ‘’retta di regressione’’ o ‘’retta interpolante’’ che ha espressione $y=a+bx$. Per comprendere i passaggi occorre sapere come si calcola una derivata ed in genere gli studenti del liceo scientifico imparano a farlo nell’ultimo anno.

Ma perché bisogna minimizzare la somma dei quadrati delle differenze? Il seguente documento in pdf si sforza di darci una motivazione. Si tratta di una piacevole lettura comprensibile ad uno studente liceale e non occorre conoscere le derivate.

Ricerca della relazione lineare

Ricapitoliamo le formule essenziali. Si vogliono determinare $a$ e $b$ in modo che la retta $y = a + bx$ approssimi, meglio di ogni altra retta, una serie di $n$ coppie di misure $(x_i, y_i)$ relative alle grandezze $X$ e $Y$ che si suppone siano legate, appunto, da una relazione di tipo lineare. Solo le misure $y_i$ sono affette da incertezze. Ecco le formule:

$$b = \frac{\sum^n_{i=1} x_i y_i - n \bar x \bar y}{\sum^n_{i=1} x_i^2 - n \bar x^2}$$

$$ a = \bar y - b \bar x$$

in cui $\bar x$ e $\bar y$ sono i valori medi di X e Y:

$$\bar x = \frac{\sum^n_{i=1} x_i }{n}$$

$$\bar y = \frac{\sum^n_{i=1} y_i }{n}$$

Purtroppo non basta determinare $a$ e $b$. Ogni calcolo serio di queste quantità va accompagnato dal calcolo delle rispettive deviazioni standard: $\sigma_a$ e $\sigma_b$. Sfortunatamente la loro determinazione è un incubo. I passi sono i seguenti:

i) calcolare la quantità $\Delta = n \sum x_i^2 - (\sum x_i)^2$

ii) calcolare la varianza delle $y_i$ rispetto alle corrispondenti teoriche ottenute dalla retta di regressione: $\sigma^2 = \frac{ 1}{ n} \sum (y_i - a -bx_i)^2$

iii) calcolare (finalmente) le deviazioni standard:

$$\sigma_b = \sigma \sqrt\frac{n}{\Delta}$$

$$\sigma_a = \sigma \sqrt\frac{\sum x_i^2}{\Delta}$$

Tieni presente che la calcolatrice scientifica, e soprattutto i calcolatori grafici, hanno delle funzioni per calcolare i parametri della retta di regressione in modo immediato a partire dai dati inseriti. Leggi il manuale della tua calcolatrice nella sezione ‘statistica’ come si attivano queste funzioni!

Relazione di proporzionalità diretta

Si tratta di un caso particolare di relazione lineare, in quanto si cerca una retta passante per l’origine. Ricorda che la legge di proporzionalità diretta è anche una legge lineare, ma non è vero il contrario. Quindi si vuole determinare $b$ in modo che la retta $y = bx$ approssimi, meglio di ogni altra retta, una serie di $n$ coppie di misure $(x_i, y_i)$ relative alle grandezze $X$ e $Y$ che si suppone siano legate, appunto, da una relazione di proporzionalità diretta. Solo le misure $y_i$ sono affette da incertezze. Ecco le formule:

$$b = \frac{\sum^n_{i=1} x_i y_i}{\sum^n_{i=1} x_i^2}$$

Per quanto riguarda il calcolo della deviazione standard $\sigma_b$ si ha:

i) calcolare la varianza delle $y_i$ rispetto alle corrispondenti teoriche ottenute dalla retta di regressione: $\sigma^2 = \frac{ 1}{ n} \sum (y_i -bx_i)^2$

ii) calcolare la deviazioni standard:

$$\sigma_b = \frac{\sigma}{ \sqrt{\sum x_i^2} }$$

esercizio

Il seguente esercizio è tratto da una delle domande della simulazione dell’esame di stato proposta dal Miur a dicembre del 2018. Si tratta di applicare quanto imparato sopra. I calcoli sono stati svolti con Excel invece di una calcolatrice grafica. Vi allego anche {{ :regressione.xlsx |il file Excel}} usato per i calcoli.

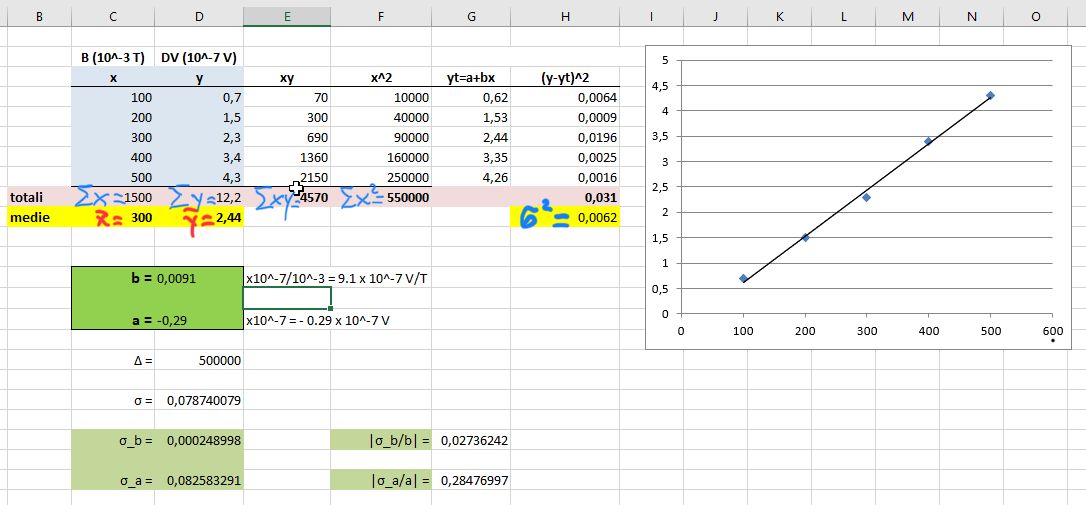
Punto 4 del testo Perché il dispositivo possa essere usato come magnetometro, è necessario procedere alla sua taratura, cioè alla misurazione di $∆𝑉_H$ in presenza di valori noti del campo magnetico $𝐵$. La seguente tabella mostra i dati sperimentali di una taratura effettuata in laboratorio:

Mostra che tali dati sono compatibili con una relazione di proporzionalità diretta tra $∆𝑉_𝐻$ e $𝐵$, traccia il grafico di taratura e fornisci una stima del valore della costante di proporzionalità k. Come valuteresti l’incertezza della stima effettuata?

Soluzione:

Il valore stimato di k coincide con quello che sopra abbiamo chiamato $b$. L’incertezza, invece, coincide col calcolo di $\sigma_b$. I calcoli e la figura sono mostrati nella figura seguente. Scarica il file Excel associato per verificare l’uso delle formule riportate sopra sia nel caso di relazione lineare che di proporzionalità diretta:

Riferimenti

• Hugh D. Young, Elaborazione statistica dei dati sperimentali, Veschi